EJERCICIOS RESUELTOS - Funciones y Derivadas
Funciones y derivadas- Matemáticas Aplicadas a las C. S. II
Sea ![]() el porcentaje de células, de un determinado tejido, afectadas por un cierto tipo de enfermedad transcurrido un tiempo
el porcentaje de células, de un determinado tejido, afectadas por un cierto tipo de enfermedad transcurrido un tiempo ![]() , medido en meses:
, medido en meses:
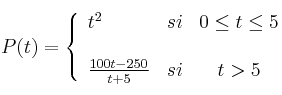
– a) Estudie la continuidad de la función P.
– b) Estudie la derivabilidad de P en
– c) Estudie la monotonía de dicha función e interprete la evolución del porcentaje de células afectadas.
– d) ¿En algún momento el porcentaje de células afectadas podría valer 50?
Se estima que el beneficio de una empresa, en millones de euros, para los próximos 10 años viene dado por la función
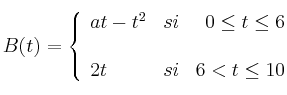
siendo ![]() el tiempo transcurrido en años.
el tiempo transcurrido en años.
– a) Calcule el valor del parámetro ![]() para que
para que ![]() sea un función continua.
sea un función continua.
– b) Para ![]() represente su gráfica e indique en qué periodos de tiempo la función crecerá o decrecerá.
represente su gráfica e indique en qué periodos de tiempo la función crecerá o decrecerá.
– c) Para ![]() indique en qué momento se obtiene el máximo beneficio en los primeros 6 años y a cuánto asciende su valor.
indique en qué momento se obtiene el máximo beneficio en los primeros 6 años y a cuánto asciende su valor.
En el mar hay una mancha producida por una erupción marina. La superficie afectada, en ![]() , viene dada por la función
, viene dada por la función 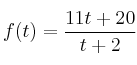 , siendo
, siendo ![]() el tiempo transcurrido desde que empezamos a observarla.
el tiempo transcurrido desde que empezamos a observarla.
– a) ¿Cuál es la superficie afectada inicialmente, cuando empezamos a medirla?
– b) Estudie si la mancha crece o decrece con el tiempo
– c) ¿Tiene algún límite la extensión de la superficie de la mancha?
En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días trabajados según la función
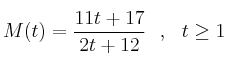 ,
,
donde ![]() es el número de días trabajados.
es el número de días trabajados.
– a) ¿Cuántos montajes realiza el primer día? ¿Cuántos días necesitará para
realizar cinco montajes diarios?
– b) ¿Qué ocurriría con el número de montajes diarios si trabajara indefinidamente?
– c) El dueño de la empresa cree que el número de montajes diarios aumenta con los días de trabajo. Estudiando la función, justifique si es cierta dicha creencia.
– d) Dibuje la gráfica de la función.
El consumo de cereales en una ciudad, en miles de toneladas, viene dado por la función ![]() , para
, para ![]() , donde
, donde ![]() representa el tiempo.
representa el tiempo.
– a) ¿En qué instante se alcanza el máximo consumo de cereales y cuántas toneladas se consumen en ese momento?
– b) ¿En qué intervalo de tiempo decrece el consumo de cereales?
– c) Represente gráficamente la función.
Se considera la función ![]()
– a) Estudie la continuidad y la derivabilidad de la función ![]()
– b) Calcule los puntos de corte de la gráfica de ![]() con los ejes de coordenadas.
con los ejes de coordenadas.
– c) Calcule las asíntotas de ![]() , en caso de que existan.
, en caso de que existan.
– a) Calcule la derivada de las funciones
![]()
– b) Obtenga la ecuación de la recta tangente a la gráfica de la función ![]() , el punto de abscisa
, el punto de abscisa ![]()
El beneficio, en miles de euros, que ha obtenido una almazara a lo largo de 50 años de vida viene dado por la expresión 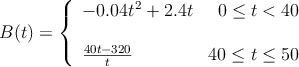
donde ![]() es el tiempo transcurrido.
es el tiempo transcurrido.
– a) Estudie la continuidad y la derivabilidad de la función ![]() en el intervalo
en el intervalo ![]() .
.
– b) Estudie la monotonía de la función ![]() y determine en qué momento fueron mayores los beneficios de la almazara, así como el beneficio máximo.
y determine en qué momento fueron mayores los beneficios de la almazara, así como el beneficio máximo.
– c) Represente la gráfica de la función y explique la evolución del beneficio.
 Matemáticas IES
Matemáticas IES