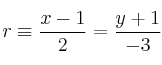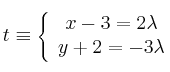EJERCICIOS RESUELTOS - Geometría en el Plano

Geometría - 1º Bach. Ciencias

Dadas las rectas:
R_1 \equiv \left\{ \begin{array}{ll} x = 3-2t \\ y = 7+t \end{array} \right.
R_2 \equiv \left\{ \begin{array}{ll} x = 1-4t \\ y = 4+3t \end{array} \right.
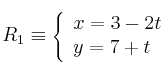
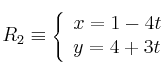
Se pide:

– una recta S paralela a R_1 por el punto (5,7)
– una perpendicular H , a R_2 por el punto (0,0)


Halla la ecuación paramétrica de una recta perpendicular a la recta 2x-3y+6=0 por el punto (1,3)


Halla un vector director y la pendiente de las rectas:

– r \equiv \frac{x-1}{2} = \frac{y+1}{-3}
– s \equiv 2x-y+1=0
– t \equiv \left\{\begin{array}{c}x-3 = 2 \lambda \\y+2 = -3 \lambda\end{array}\right.


Sean L1 y L2 las rectas de ecuación

L1 \longrightarrow (c+1)x - 4y - (c-1) = 0
L2 \longrightarrow y= \frac{-1}{3} x + 1

donde c \in R

a) Determinar el valor de c para el cual la recta L1 ea perpendicular a la recta L2. Escribir la ecuación de la recta L1

b) Hallar analíticamente el punto de intersección de las rectas L1 y L2 y verificar gráficamente el resultado hallado.

c) Encontrar la ecuación de la recta L que es paralela a la recta L1 y pasa por el punto P= ( -1/3 , 1/3)


Dados los puntos P(0,4) y Q(-6,0) , halla la ecuación paramétrica de la recta perpendicular al segmento \overline{PQ} en su punto medio.


Halla la posición relativa de las rectas:

r \rightarrow -x+3y+4=0
s \rightarrow 3x-9y-12=0


Halla la posición relativa de las rectas:

r \rightarrow 5x+y+3=0
s \rightarrow x-2y+16=0


Usa el producto escalar para hallar el ángulo que forman los vectores \vec{u}(6,2) y \vec{v}(-1,3)


Si P(5,-2) es el punto medio del segmento \overline{AB} , calcula las coordenadas de B , siendo A(2,1)


Dada la recta 4x + 3y - 6 = 0, escribe la ecuación de la recta perpendicular a ella en el punto de corte con el eje de ordenadas.


  •  (1883) Ejercicios Resueltos
1º BACH. CIENCIAS 1º BACH. SOC. 1º ESO 2º BACH. CIENCIAS 2º BACH. SOC. 2º ESO 3º ESO 4º ESO