-
Dadas las matrices:
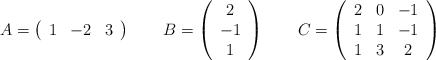
– a) Justifica si la matriz C tiene inversa
– b) Halla la inversa de C
– c) Resuelve la ecuación matricial 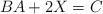
-
En un edificio residencial hay tres tipos de viviendas: L3, L4 y L5. Las viviendas L3 tienen 4 ventanas pequeñas y 3 ventanas grandes; las viviendas L4 tienen 5 ventanas pequeñas y 4 grandes; y las L5, 6 ventanas pequeñas y 5 grandes. Cada ventana pequeña tiene 2 cristales y 4 bisagras, y las grandes, 4 cristales y 6 bisagras.
– a) Escribe una matriz que describa el número y el tamaño de las ventanas de cada vivienda y otra que exprese el número de cristales y bisagras de cada tipo de ventana.
– b) Calcula la matriz que expresa el número de cristales y de bisagras de cada tipo de vivienda
-
Se considera la matriz 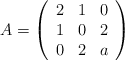
a) Determine para qué valores del parámetro  , la matriz
, la matriz  tiene inversa.
tiene inversa.
b) Para 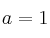 , calcule la inversa de
, calcule la inversa de  .
.
c) Para 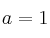 , resuelva la ecuación matricial
, resuelva la ecuación matricial 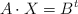 , siendo
, siendo 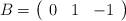
-
Se consideran las matrices
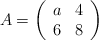
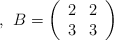 y
y 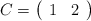
a) Calcule el valor del parámetro  para que la matriz
para que la matriz  no tenga inversa.
no tenga inversa.
b) Para 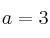 , resuelva la ecuación matricial
, resuelva la ecuación matricial 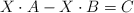 .
.
c) Para 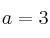 , compruebe que
, compruebe que 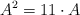 y exprese
y exprese 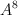
en función de la matriz  .
.
-
Averigua las dimensiones de las matrices  ,
,  y
y 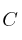 para que se cumplan todas las condiciones siguientes:
para que se cumplan todas las condiciones siguientes:
a) Se pueda sumar  con una matriz
con una matriz 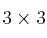
b) Se pueda multiplicar 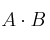 pero no
pero no 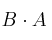
c) Se pueda calcular 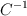
d)  tenga el mismo número de columnas que
tenga el mismo número de columnas que 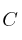 de filas.
de filas.
e) El rango de 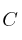 es
es 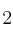 y coincide con su número de columnas.
y coincide con su número de columnas.
 matrices
matrices