EJERCICIOS RESUELTOS - Funciones

Mat. Aplicadas C. Sociales I - Funciones

Halla los puntos de corte con los ejes de las siguientes funciones:

– $f(x) = 3x + 12$
– $g(x) = (x - 2) \cdot (x - 4)$
– $h(x) = x^2 + 4x - 5$

Dadas las funciones 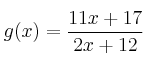$f(x)=x^2-5x+6$ ; $g(x)=\frac{11x+17}{2x+12}$ , se pide para ambas funciones:

– a) Hallar su dominio
– b) Puntos de corte con los ejes de coordenadas
– c) Representación gráfica

Dibuja la gráfica de las siguientes expresiones algebraicas (reflejando todos los cálculos necesarios antes de dibujarlas).

– a) $y = -x +5$
– b) $y = x^2$
– c) $y = 5 - \frac{x}{2}$

Solución

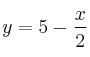
Esboza la gráfica de la función que se ajusta a las siguientes condiciones:

– el dominio es $\mathbb{R} - \{5\}$
– la imagen es todo $\mathbb{R}$
– corta a los ejes en los puntos $(-5, 0), (0, 3), (2, 0)$ y $(4, 0)$
– alcanza un máximo en el punto $(-2, 4)$ y otro en $(6, -2)$
– alcanza un mínimo en $(3, -2)$
– tiene una asíntota vertical en $x = 5$
– cuando $x \longrightarrow 5^-$ , $f(x) \longrightarrow +\infty$

Solución

Sea la función $f(x)=\frac{x+1}{x+2}$
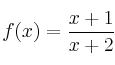
– a) Representa gráficamente la función
– b) Calcula asíntotas, dominio, corte con los ejes y monotonía

Solución

Sea la función:

$f(x)= \left\{ \begin{array}{lcc} 5 & si & x \leq 2 \\ \\ x^2-6x+10 & si & 2 < x < 5 \\ \\ 4x-15 & si & x \geq 5 \end{array} \right.$

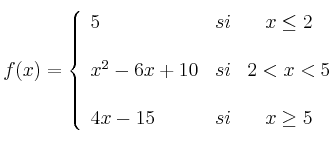
– a) Representación gráfica
– b) Indica Dominio, Corte con los ejes, Asíntotas, Monotonía y Extremos

Solución

Sea la función 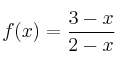$f(x) = \frac{3-x}{2-x}$

– a) Calcula sus asíntotas
– b) Estudia su monotonía
– c) Represéntala gráficamente

Solución

Sea la función 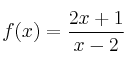$f(x)=\frac{2x+1}{x-2}$

– a) Representa gráficamente la función
– b) Calcula asíntotas, dominio, corte con los ejes y monotonía

Solución

El valor, en miles de euros, de las existencias de una empresa en función del tiempo t, en años, viene dado por la función:

$f(t)=-4t^2+60t-15 \:,\:\:\:\:\:\: 1 \leq t \leq 8$

– a) ¿Cuál será el valor de las existencias para $t=2$ ? ¿Y para $t=4$ ?
– b) ¿Cuál es el valor máximo de las existencias? ¿En qué instante se alcanza?
– c) ¿En qué instante el valor de las existencias es de 185000 euros?

Solución

El beneficio obtenido por la producción y venta de x kilogramos de un artículo viene dado por la función:

$B(x)=-0.01x^2+3.6x-180$

– a) Representa gráficamente esta función.
– b) Determina el número de kilogramos que hay que producir y vender para que el beneficio sea máximo.
– c) Determina cuántos kilogramos se deben producir y vender, como máximo, para que la empresa no tenga pérdidas.

Más páginas de Ejercicios