EJERCICIOS RESUELTOS - Geometría en el Espacio
Ejercicios de Geometría en el espacio. Bachillerato
Comprueba que los siguientes vectores forman una base:
![]()
Comprueba que los siguientes vectores forman una base:
![]()
Considera los puntos ![]() ,
, ![]() y
y ![]()
– a) Determina los vectores ![]() y
y ![]()
– b) Calcula la distancia entre los puntos ![]() y
y ![]()
– c) Calcula el producto escalar 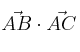
– d) Calcula el producto vectorial 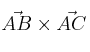
– e) Halla el área del triángulo determinado por los puntos ![]() ,
, ![]() y
y ![]()
Consideramos los puntos ![]() ,
, ![]() y
y ![]() .
.
– a) Calcula ![]() (distancia entre los puntos A y B)
(distancia entre los puntos A y B)
– b) 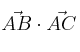 (producto escalar)
(producto escalar)
– c) Calcula el perímetro del triángulo de vértices A, B y C
– d) Halla el área del triángulo de vértices A, B y C
Halla el valor de ![]() para que los vectores
para que los vectores ![]() y
y ![]() sean ortogonales
sean ortogonales
Dados los vectores ![]() ;
; ![]() ;
; ![]() se pide:
se pide:
a) ¿Forman una base de ![]() ? ¿Por qué?
? ¿Por qué?
b) Realiza las siguientes operaciones:
- b1)
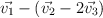
- b2)
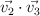
- b3)
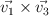
Considera los puntos ![]() ,
, ![]() ,
, ![]() y
y ![]()
– a) Calcula el módulo de los vectores ![]() y
y ![]()
– b) Los vectores ![]() ,
, ![]() y
y ![]() ¿son linealmente independientes?
¿son linealmente independientes?
– c) Calcula el producto escalar 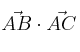
– d) Halla el área del triángulo determinado por los puntos ![]() ,
, ![]() y
y ![]()
Calcula el volumen del paralelepípedo definido por los puntos ![]() ,
, ![]() ,
, ![]() y
y ![]()
Calcula el volumen del tetraedro ABCD y la altura del vértice B sobre la cara ACD con los siguientes datos:
![]() (producto mixto)
(producto mixto)
![]() (módulo de producto vectorial)
(módulo de producto vectorial)
![]()
![]()
![]()
 Matemáticas IES
Matemáticas IES