EJERCICIOS RESUELTOS - Programación Lineal
Matemáticas Aplicadas a las Ciencias Sociales II (2º Bachillerato)
Desde dos almacenes A y B, se tiene que distribuir fruta a tres mercados de la ciudad. El almacén A dispone de 10 toneladas de fruta diarias y el B de 15 toneladas, que se reparten en su totalidad. Los dos primeros mercados necesitan, diariamente, 8 toneladas de fruta, mientras que el tercero necesita 9 toneladas diarias.
El coste del transporte desde cada almacén a cada mercado viene dado por el siguiente cuadro:

Planificar el transporte para que el coste sea mínimo.
Un taller fabrica y vende dos tipos de alfombras, de seda y de lana. Para la elaboración de una unidad se necesita un trabajo manual de 2 horas para el primer tipo y de 3 horas para el segundo y de un trabajo de máquina de 2 horas para el primer tipo y de 1 hora para el segundo. Por cuestiones laborales y de planificación, se dispone de hasta 600 horas al mes para el trabajo manual y de hasta 480 horas al mes para el destinado a la máquina. Si el beneficio por unidad para cada tipo de alfombra es de 150 € y 100 €, respectivamente, ¿cuántas alfombras de cada tipo debe elaborar para obtener el máximo beneficio? ¿A cuánto asciende el mismo?
En una carpintería, que consta de tres secciones, se construyen mesas y conjuntos de 4 sillas. En la primera sección se cortan las piezas que conforman los muebles, invirtiéndose una hora en el conjunto de las 4 sillas y tres horas en la mesa. En la segunda sección se realiza el ensamblaje de las piezas, empleándose 1 hora y 20 minutos, tanto para las sillas como para la mesa. Por último, en la tercera sección se pulen los muebles, tardándose 2 horas y 30 minutos en finalizar las 4 sillas y sólo 8/7 de hora en la mesa. Debido a las características de la empresa, sólo se puede trabajar un máximo de 61 horas semanales en las secciones 2ª y 3ª y 60 horas en la 1ª. Sabiendo que las ganancias por el conjunto de las 4 sillas y la mesa son respectivamente, 800 € y 600 €, organiza tú mismo cómo debiera ser la producción para que así los beneficios fuesen máximos.
Se quiere organizar un puente aéreo entre dos ciudades, con plazas suficientes de pasaje y carga, para transportar 1600 personas y 96 toneladas de equipaje. Los aviones disponibles son de dos tipos: 11 del tipo A y 8 del tipo B. La contratación de un avión del tipo A cuesta 4 millones de pts y puede transportar 200 personas y 6 toneladas de equipaje; la contratación de uno del tipo B cuesta 1 millón de pts y puede transportar 100 personas y 15 toneladas de equipaje.
¿Cuántos aviones de cada tipo deben utilizarse para que el coste sea mínimo?.
Sea el recinto definido por las siguientes inecuaciones:
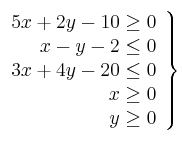
– a) Dibuje dicho recinto y determine sus vértices.
– b) Determine en qué punto de ese recinto alcanza la función ![]() el máximo valor.
el máximo valor.
Una imprenta local edita periódicos y revistas. Para cada periódico necesita un cartucho de tinta negra y otro de color, y para cada revista uno de tinta negra y dos de color. Si sólo dispone de 800 cartuchos de tinta negra y 1100 de color, y si no puede imprimir más de 400 revistas, ¿cuánto dinero podrá ingresar como máximo, si vende cada periódico a 0.9 euros y cada revista a 1.2 euros?
Un Ayuntamiento concede licencia para la construcción de una urbanización de a lo sumo 120 viviendas, de dos tipos A y B.
Para ello la empresa constructora dispone de un capital máximo de 15 millones de euros, siendo el coste de construcción de la vivienda de tipo A de 100000 euros y la de tipo B 300000 euros.
Si el beneficio obtenido por la venta de una vivienda de tipo A asciende a 20000 euros y por una de tipo B a 40000 euros, ¿cuántas viviendas de cada tipo deben construirse para obtener un beneficio máximo?
Consideramos el recinto del plano limitado por las siguientes inecuaciones:
![]()
– (a) Represente el recinto y calcule sus vértices.
– (b) Halle en qué puntos de ese recinto alcanza los valores máximo y mínimo la función ![]()
(a) Represente gráficamente la región determinada por las siguientes restricciones:
![]()
(b) Calcule el máximo de la función ![]() en el recinto anterior e indique dónde se alcanza.
en el recinto anterior e indique dónde se alcanza.
En un examen de Matemáticas se propone el siguiente problema:
"Indique dónde se alcanza el mínimo de la función ![]() en la región determinada por las restricciones
en la región determinada por las restricciones ![]() ;
; ![]() ;
; ![]() ."
."
– (a) Resuelva el problema
– (b) Ana responde que se alcanza en ![]() y Benito que lo hace en
y Benito que lo hace en ![]() . ¿Es cierto que el mínimo se alcanza en
. ¿Es cierto que el mínimo se alcanza en ![]() ?. ¿Es cierto que se alcanza en
?. ¿Es cierto que se alcanza en ![]() ?.
?.
 Matemáticas IES
Matemáticas IES