-
Dadas las matrices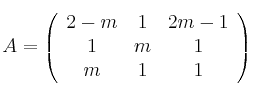 
, 
, 
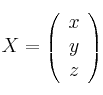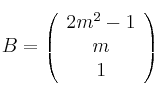, considera el sistema de ecuaciones lineales dado por 
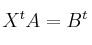, donde 
, 
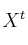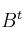denotan las traspuestas. Discútelo según los distintos valores de m
-
a) Dadas las inecuaciones
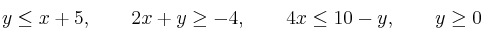
represente el recinto que limitan y calcule sus vértices.
b) (0.7 puntos) Obtenga el máximo y el mínimo de la función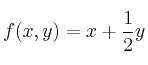 
en el recinto anterior, así como los puntos en los que se alcanzan.
-
a) Represente el recinto definido por las siguientes inecuaciones:
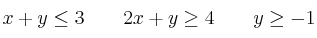
b) Razone si el punto (2, 1) pertenece al recinto anterior.
c) Obtenga los vértices del recinto y los valores mínimo y máximo de la función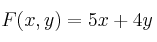 
en ese recinto, indicando en qué puntos se alcanzan.
d) Razone si la función F puede alcanzar el valor 9 en el recinto anterior.
-
a) Plantee, sin resolver, las restricciones de este problema e indique la función a optimizar:
"Un ganadero alimenta a sus ovejas con maíz y pienso. Cada kilogramo de maíz aporta 600 g de hidratos de carbono y 200 g de proteínas, mientras que cada kilogramo de pienso aporta 300 g de hidratos de carbono y 600 g de proteínas. Cada oveja necesita diariamente como mínimo 1800 g de hidratos de carbono y 2400 g de proteínas. Si 1 kg de maíz cuesta 0.50 euros y 1 kg de pienso cuesta 0.25 euros, calcule cuántos kilogramos de cada producto tendría que comprar el ganadero para alimentar cada día a una oveja con un gasto mínimo".
b) Represente el recinto limitado por las siguientes restricciones, calculando sus vértices
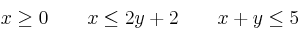
Calcule el máximo de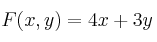 
en ese recinto, así como el punto donde se alcanza
.
-
Considera la función f definida por
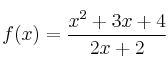para 
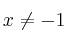
– a) Estudia y halla las asíntotas de la gráfica de f.
– b) Determina los intervalos de crecimiento y decrecimiento de f.
Matemáticas IES
selectividad
selectividad