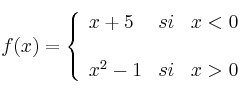EJERCICIOS RESUELTOS - Funciones (I)
Funciones (I) - 1º Bachillerato de Ciencias
Halla el dominio de la función: ![]()
Halla el dominio de la función 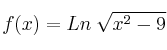
Indica el dominio y corte con los ejes de coordenadas de las siguientes funciones:
– a) 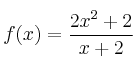
– b) ![]()
– c) 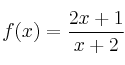
– d) ![]()
– e) 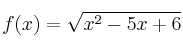
Encontrar dominio y rango de la siguiente función y graficar
![]()
Halla los extremos relativos de la función ![]()
Halla el valor de ![]() para que la siguiente función sea continua:
para que la siguiente función sea continua:
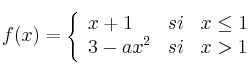
Represente gráficamente la función para el valor de
Un agente antibacteriano agregado a una población de bacterias causa disminución en el tamaño de esta. Si la población t minutos después de agregado el agente es ![]() , donde
, donde ![]() representa la cantidad inicial. Determine:
representa la cantidad inicial. Determine:
– a) La función de cambio de la población en el tiempo t si la población inicial es de ![]() bacterias.
bacterias.
– b) ¿Después de qué periodo de tiempo la población ha disminuido ![]() unidades?
unidades?
La temperatura de un pastel que se saca a enfriar de un horno a 200 grados centígrados, es una función del tiempo (medida en minutos) dada por
![]()
donde
– a) Si después de 10 minutos el pastel está a 40 grados, calcula la constante ![]()
– b) Encuentra la rapidez (en grados/minutos) con la que decrece la temperatura, cuando recién se saca del horno.
– c) Describe que pasa con la temperatura del pastel para ![]() muy grande
muy grande
 Matemáticas IES
Matemáticas IES