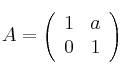EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas

Matrices, Determinantes y Sistemas de Ecuaciones - 2º Bach. Sociales

En un edificio residencial hay tres tipos de viviendas: L3, L4 y L5. Las viviendas L3 tienen 4 ventanas pequeñas y 3 ventanas grandes; las viviendas L4 tienen 5 ventanas pequeñas y 4 grandes; y las L5, 6 ventanas pequeñas y 5 grandes. Cada ventana pequeña tiene 2 cristales y 4 bisagras, y las grandes, 4 cristales y 6 bisagras.

– a) Escribe una matriz que describa el número y el tamaño de las ventanas de cada vivienda y otra que exprese el número de cristales y bisagras de cada tipo de ventana.
– b) Calcula la matriz que expresa el número de cristales y de bisagras de cada tipo de vivienda

Solución

Sea la matriz $A = \left( \begin{array}{cc} 1 & a \\ 0 & 1 \end{array} \right)$

Obtenga la matriz $A^{2014}$

Solución

Sabiendo que A y B son dos matrices de orden 2, tales que |A| = - 2 y |B| = 4, calcula:

– a) $|AB^t|$
– b) $|A^t|$
– c) $|B^{-1}|$
– d) $|A^{-1} \cdot B|$
– e) $|3A|$

Solución

Calcula la inversa de la matriz A por el método de Gauss-Jordan
$A = \left( \begin{array}{ccc} 1 & 3 & 4 \\ 0 & -1 & 2 \\ 2 & 5 & 0 \end{array} \right)$

Solución

Sea la matriz 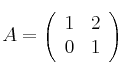$A = \left( \begin{array}{cc} 1 & 2 \\ 0 & 1 \end{array} \right)$
Hallar las matrices B que conmuten con A; es decir: $A \cdot B = B \cdot A$

Solución

Dado el siguiente sistema de ecuaciones,
$\left. \begin{array}{ccc} 2x - 3y + 4z & = & 1 \\ x-y & = & 5 \\ -y+x-2 & = & 3z \end{array} \right\}$

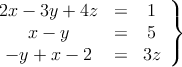
a) Escribe la matriz de los coeficientes y la matriz ampliada del sistema anterior.
b) Convierte, a través de transformaciones elementales, la matriz ampliada anterior en matriz escalonada.

Solución

Dadas las siguientes matrices
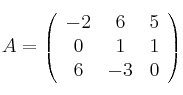$A=\left( \begin{array}{ccc} -2 & 6 & 5 \\ 0 & 1 & 1 \\ 6 & -3 & 0 \end{array} \right)$ y $B=\left( \begin{array}{ccc} -3 & 0 & 1 \\ -1 & -2 & 0 \\ 2 & 1 & -1 \end{array} \right)$

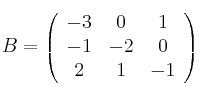
– a) Calcula el rango de A. ¿Existe la inversa de A? ¿Por qué?
– b) Calcula, si es posible, la inversa de la matriz B.

Solución

Dadas las matrices:

$A=\left( \begin{array}{ccc} 1&-2&3 \end{array}\right) \qquad B=\left( \begin{array}{c} 2\\-1\\1 \end{array}\right) \qquad C=\left( \begin{array}{ccc} 2&0&-1\\1&1&-1\\1&3&2 \end{array}\right)$

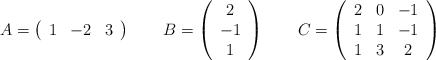
– a) Justifica si la matriz C tiene inversa
– b) Halla la inversa de C
– c) Resuelve la ecuación matricial $BA + 2X = C$

Solución

Dadas las siguientes matrices
$A=\left( \begin{array}{ccc} 1 & -2 & 0 \\ 3 & 1 & -1 \\ 0 & -2 & 2 \end{array} \right) \qquad B=\left( \begin{array}{ccc} 3 & 1 & -1 \\ -4 & 0 & 2 \end{array} \right) \qquad C=\left( \begin{array}{ccc} 0 & 2 & -2 \\ 1 & 3 & 0 \end{array} \right)$

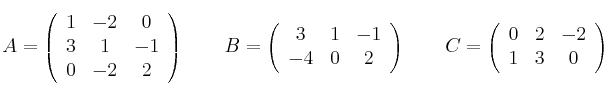
Indica razonadamente cuáles de las siguientes operaciones se pueden hacer y cuáles no y realiza todas aquellas que sí se puedan:

– a) $A^t + B$
– b) $A \cdot C^t$
– c) $|A|$
– d) $|C|$
– e) $C - 2B$

Solución

Una empresa tiene tres factorías, F1, F2, F3, en las que se fabrican diariamente tres tipos diferentes de productos, A, B y C, como se indica a continuación:

F1: 200 unidades de A, 40 de B y 30 de C.

F2: 20 unidades de A, 100 de B y 200 de C.

F3: 80 unidades de A, 50 de B y 40 de C.

Cada unidad de A que se vende proporciona un beneficio de 5 euros; por cada unidad de B, se obtienen 20 euros de beneficio; y por cada una de C, 30 euros.

Sabiendo que la empresa vende toda la producción diaria, obtén matricialmente el beneficio diario obtenido con cada una de las tres factorías.

Más páginas de Ejercicios