EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas
Matrices, Determinantes y Sistemas de Ecuaciones - 2º Bach. Sociales
El dueño de una librería va a poner a la venta libros de tres géneros diferentes: idiomas, infantil e informática.
El dueño se ha fijado como objetivo vender 150 ejemplares y quiere obtener unos ingresos por venta de 2300 €. El precio de los libros de idiomas los ha fijado a 20€/libro, los de informática a 15€/libro y a los de infantil les va a hacer un descuento del 30% sobre 10€ que costaban el año anterior. Además sabe por ventas de otros años, que el número de libros de temática infantil va a ser la mitad de los libros de temática de idiomas. Teniendo en cuenta las condiciones descritas, ¿cuántos ejemplares debería vender de cada género para obtener su objetivo?
A continuación te pedimos que respondas a cada una de las siguientes cuestiones.
1.- Identifica y nombra cada una de las incógnitas que aparecen.
2.- Determina el precio que cuesta cada libro según su género, teniendo en cuenta que para calcular el precio de los libros de temática infantil se le va a aplicar el 30% de descuento al precio de venta del año pasado que fue de 10€ cada libro.
3.- Plantea un sistema de tres ecuaciones con tres incógnitas.
4.- Resuelve el sistema de ecuaciones por el método de Gauss matricialmente.
Un cliente de un supermercado ha pagado un total de 156 euros por 24 litros
de leche, 6 kg de jamón serrano y 12 litros de aceite de oliva.
Plantee y resuelva un sistema de ecuaciones para calcular el precio unitario de cada artículo, sabiendo que 1 litro de aceite cuesta el triple que un litro de leche y que 1 kg de jamón cuesta igual que 4 litros de aceite más 4 litros de leche.
Sean las matrices
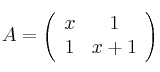
![]()
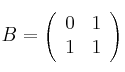
– a) Encuentre el valor o valores de x de forma que ![]()
– b) Igualmente para que ![]()
– c) Determine x para que ![]()
Sean las matrices
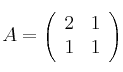 ,
,
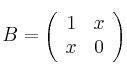 y
y
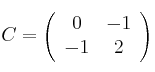
– (a) Encuentre el valor o valores de ![]() de forma que
de forma que ![]()
– (b) Igualmente para ![]()
– (c) Determine ![]() para que
para que ![]()
Sean las matrices
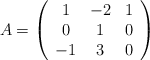 ,
,
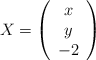 e
e
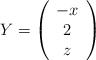
– (a) Determine la matriz inversa de ![]()
– (b) Halle los valores de ![]() ,
, ![]() ,
, ![]() para los que se cumple
para los que se cumple ![]()
Sean las matrices:
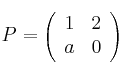 ,
,
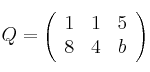 y
y
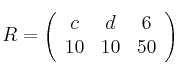
– a) Calcule, si es posible, ![]() y
y ![]() , razonando la respuesta
, razonando la respuesta
– b) ¿Cuánto deben valer las constantes a, b, c y d para que ![]() ?
?
Sean las matrices
![]()
a) Efectúe, si es posible, los siguientes productos:
– a1) ![]()
– a2) ![]()
– a3) ![]()
b) Resuelva la siguiente ecuación matricial ![]()
Sean las matrices
![]()
,
![]()
,
![]()
– a) Resuelva la ecuación matricial ![]()
– b) Determine en cada caso la dimensión de la matriz D para que se puedan realizar las siguientes operaciones: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
– a) Determine los valores de x e y que hacen cierta la igualdad
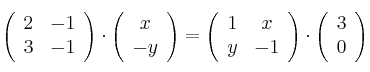
– b) Resuelva la ecuación matricial
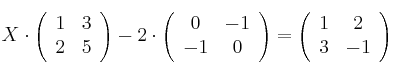
Se consideran las matrices
![]()
![]() y
y ![]()
a) Calcule el valor del parámetro ![]() para que la matriz
para que la matriz ![]() no tenga inversa.
no tenga inversa.
b) Para ![]() , resuelva la ecuación matricial
, resuelva la ecuación matricial ![]() .
.
c) Para ![]() , compruebe que
, compruebe que ![]() y exprese
y exprese ![]()
en función de la matriz ![]() .
.
 Matemáticas IES
Matemáticas IES