EJERCICIOS RESUELTOS - Geometría en el Espacio
Ejercicios de Geometría en el espacio. Bachillerato
Se sabe que las rectas:
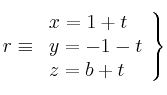
y
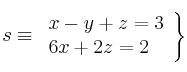
están contenidas en un mismo plano
– (a) Calcula ![]()
– (b) Halla la ecuación del plano que contiene a las rectas ![]() y
y ![]()
Se considera la recta ![]() definida por
definida por ![]() ,
, ![]() , y la recta
, y la recta ![]() definida por
definida por 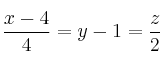
– (a) Halla el valor de ![]() para el que
para el que ![]() y
y ![]() son perpendiculares.
son perpendiculares.
– (b) Deduce razonadamente si existe algún valor de ![]() para el que
para el que ![]() y
y ![]() son paralelas.
son paralelas.
Considera los puntos ![]() ,
, ![]() ,
, ![]() y
y ![]() .
.
– (a) Calcula la ecuación del plano ![]() que contiene a los puntos
que contiene a los puntos ![]() ,
, ![]() y
y ![]()
– (b) Halla el punto simétrico de ![]() respecto del plano
respecto del plano ![]() .
.
Considera el punto ![]() y la recta
y la recta ![]() definida por las ecuaciones
definida por las ecuaciones
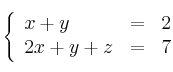
– a) Halla la ecuación del plano perpendicular a r que pasa por A
– b) Calcula la distancia del punto A a la recta r
Considera el punto ![]() , la recta
, la recta ![]() definida por
definida por 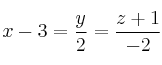 y la recta
y la recta ![]() definida por
definida por ![]() .
.
– (a) Estudia la posición relativa de ![]() y
y ![]()
– (b) Halla la ecuación del plano que pasando por ![]() es paralelo a
es paralelo a ![]() y
y ![]() .
.
Se considera la recta r definida por
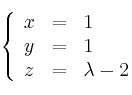
y la recta s definida por
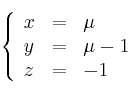
Halla la ecuación de la recta perpendicular común a r y s
Sea la recta ![]() definida por
definida por
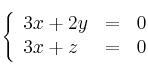
– a) Determine la ecuación del plano perpendicular a ![]() que pasa por el punto
que pasa por el punto ![]()
– b) Halla los puntos de r cuya distancia al origen es de 4 unidades
Halla la ecuación del plano que es paralelo a la recta ![]() de ecuaciones
de ecuaciones
![]()
y contiene a la recta ![]() definida por
definida por
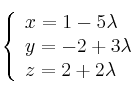
Considera los planos ![]() ,
, ![]() y
y ![]() dados respectivamente por las ecuaciones
dados respectivamente por las ecuaciones
![]() ,
, ![]() y
y ![]()
– a) ¿Cuánto ha de valer ![]() para que no tengan ningún punto en común?
para que no tengan ningún punto en común?
– b) Para ![]() , determina la posición relativa de los planos.
, determina la posición relativa de los planos.
Halla el punto simétrico de ![]() respecto de la recta
respecto de la recta ![]() de ecuación
de ecuación
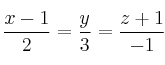
 Matemáticas IES
Matemáticas IES