EJERCICIOS RESUELTOS - Funciones, Derivadas e Integrales
Análisis matemático: Funciones, Límites, Derivadas e Integrales
a) Hallar los valores de ![]() y
y ![]() para que la función
para que la función
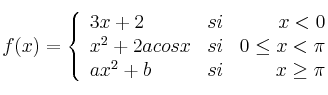
sea continua para todo valor de ![]()
b) Estudia la derivabilidad para los anteriores valores de ![]() y
y ![]()
Dada la función ![]() , se pide:
, se pide:
a) Dominio de definición y puntos de corte con los ejes.
b) Estudio de las asíntotas (verticales, horizontales y oblicuas).
c) Intervalos de crecimiento y decrecimiento. Extremos (máximos y mínimos).
d) Representación gráfica aproximada.
Para la función ![]() , se pide:
, se pide:
a) Dominio de definición y puntos de corte con los ejes.
b) Estudio de las asíntotas (verticales, horizontales y oblicuas).
c) Intervalos de crecimiento y decrecimiento. Extremos (máximos y mínimos).
d) Representación gráfica aproximada.
Sea la función dada por
![]()
a) Demuestre que es continua en todo R
b) Determine si la función es derivable en ![]() y, en caso afirmativo, calcule
y, en caso afirmativo, calcule ![]() .
.
Dada la función ![]() , se pide:
, se pide:
a) Dominio de definición y cortes con los ejes.
b) Estudio de las asíntotas (verticales, horizontales y oblicuas).
c) Intervalos de crecimiento y decrecimiento. Extremos (máximos y mínimos).
d) Representación gráfica aproximada.
Dada la función ![]() , se pide:
, se pide:
a) Determine el punto de la gráfica de f para el cual la recta tangente es paralela a la bisectriz del primer cuadrante. Calcule la ecuación de dicha recta.
b) Determine el punto de la gráfica de f para el cual la recta tangente es paralela al eje OX. Calcule la ecuación de dicha recta.
Considere la función ![]()
Determine los valores de los parámetros ![]() y
y ![]() para los cuales la función
para los cuales la función ![]() es continua y derivable en todo R.
es continua y derivable en todo R.
Para la función 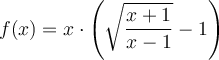 , se pide:
, se pide:
a) Dominio de definición
b) Calcule ![]() . ¿Es posible calcular también
. ¿Es posible calcular también ![]() ?. Justifique la respuesta
?. Justifique la respuesta
c) Calcule ![]()
– Dibuje la región encerrada por las curvas ![]() y
y ![]()
– Encuentre el área de dicha región
De las siguientes funciones indica para cada una: tipo de función y dominio.
– a) ![]()
– b) 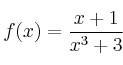
– c) ![]()
– d) ![]()
– e) ![]()
 Matemáticas IES
Matemáticas IES