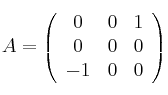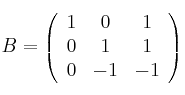EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas
Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
Considera la matriz
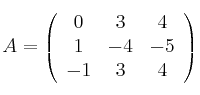
– (a) Siendo ![]() la matriz identidad
la matriz identidad ![]() y
y ![]() la matriz nula
la matriz nula ![]() , prueba que
, prueba que ![]()
– (b) Calcula ![]()
Considera el sistema
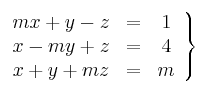
– a) Discútelo según los valores de ![]()
– b) ¿Cuál es, según los valores de ![]() , la posición relativa de los planos cuyas ecuaciones respectivas son las tres que forman el sistema?
, la posición relativa de los planos cuyas ecuaciones respectivas son las tres que forman el sistema?
– a) Clasifica el siguiente sistema según los valores del parámetro ![]()
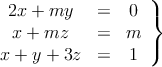
– b) Resuelve el sistema anterior para ![]()
En el sector de las aceitunas sin hueso, tres empresas A, B y C, se encuentran en competencia. Calcula el precio por unidad dado por cada empresa sabiendo que verifican las siguientes relaciones:
– El precio de la empresa A es 0,6 euros menos que la media de los precios establecidos por B y C.
– El precio dado por B es la media de los precios de A y C.
– El precio de la empresa C es igual a 2 euros mas 2/5 del precio dado por A mas 1/3 del precio dado por B.
Considera las matrices
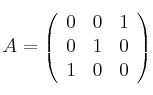
,
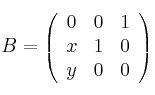
– a) Calcula la matriz inversa de ![]()
– b) Calcula ![]() y
y ![]()
– c) Determina ![]() e
e ![]() tal que
tal que ![]()
Considera el siguiente sistema de ecuaciones
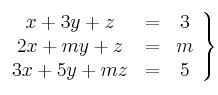
– a) Determina, si es posible, un valor de ![]() para que el correspondiente sistema tenga una y sólo una solución.
para que el correspondiente sistema tenga una y sólo una solución.
– b) Determina, si es posible, un valor de ![]() para que el correspondiente sistema tenga al menos dos soluciones.
para que el correspondiente sistema tenga al menos dos soluciones.
– c) Determina, si es posible, un valor de ![]() para que el correspondiente sistema no tenga solución.
para que el correspondiente sistema no tenga solución.
Considera el sistema de ecuaciones
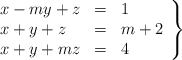
– a) Clasifícalo según los valores del parámetro ![]()
– b) Resuélvelo cuando sea compatible indeterminado
Álvaro, Marta y Guillermo son tres hermanos. Álvaro dice a Marta: si te doy la quinta parte del dinero que tengo, los tres hermanos tendremos la misma cantidad. Calcula lo que tiene cada uno si entre los tres juntan 84 euros.
Considera el sistema de ecuaciones:
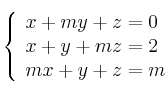
– (a) ¿Para qué valor de ![]() el sistema tiene al menos dos soluciones?
el sistema tiene al menos dos soluciones?
– (b) ¿Para qué valores de ![]() el sistema admite solución en la que
el sistema admite solución en la que ![]() ?
?
 Matemáticas IES
Matemáticas IES