EJERCICIOS RESUELTOS - Funciones, Derivadas e Integrales

Análisis matemático: Funciones, Límites, Derivadas e Integrales

Sea f : R \longrightarrow R la función definida por

f(x)= \left\{ \begin{array}{lcc} \frac{1}{x-1} & si & x < 0 \\ \\ x^2-3x-1 & si & x \geq 0 \end{array} \right.


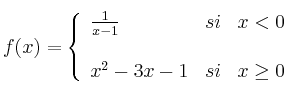
– a) Estudia la continuidad y dervabilidad
– b) Determina sus asíntotas y sus extremos relativos
– c) Esboza la gráfica de f


Se sabe que la función f: R \longrightarrow R definida por

f(x) = ax^3+bx^2+cx+d


tiene extremos relativos en (0,0) y en (2,2). Calcula a,b,c,d


En una empresa los ingresos (en euros) dependen de la edad. Si la edad, x, es de 18 a 50 a ños, los ingresos vienen dados por la fórmula -x^2 + 70x, mientras que para edades iguales o superiores a 50 años los ingresos están determinados por la expresión,

\frac{400x}{x-30}

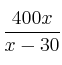
Calcula cuál es el máximo de los ingresos y a qué edad se alcanza.


Se desea construir un depósito cilíndrico cerrado de área total igual a 54 \: m^2. Determina el radio de la base y la altura del cilindro para que este tenga volumen máximo.


Sea la función f \: : \: R \: \longrightarrow \: R definida por f(x)=e^x (x^2-x+1)

– a) Calcula \lim_{x \rightarrow - \infty} f(x) y \lim_{x \rightarrow + \infty} f(x)
– b) Halla los extremos relativos de f (abscisas donde se obtienen y valores que se alcanzan), determinando si son máximos o mínimos.
– c) Determina las abscisas de los puntos de inflexión de la gráfica de f.


Sea f \: : \: (-\infty, 1) \rightarrow R la función definida por
f(x)= \left\{ \begin{array}{lcc} x+2e^{-x} & si & x \leq 0 \\ \\ \\ a \sqrt{b-x} & si & x > 0 \end{array} \right.
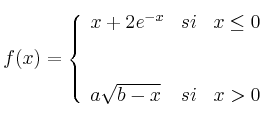
– a) Determina a y b sabiendo que f es derivable en todo su dominio.
– b) Halla la ecuación de la recta tangente y de la recta normal a la gráfica f en el punto de abcisa x=0


Sea g: \: R \rightarrow R definida por g(x)=ln(x^2+1). Calcula la primitiva de g cuya gráfica pasa por el origen de coordenadas.


Sea f : R \longrightarrow R la función definida por f(x) = e^x \cdot cos(x)

– a) Calcula la ecuación de la recta tangente a la gráfica de f en el punto de abcisa x=0
– b) Calcula la primitiva de f cuya gráfica pasa por el punto (0,0)


Considera la función f definida por
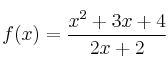f(x)=\frac{x^2+3x+4}{2x+2} para x \neq -1

– a) Estudia y halla las asíntotas de la gráfica de f.
– b) Determina los intervalos de crecimiento y decrecimiento de f.


Sea f : R \rightarrow R la función definida por f(x)=e^x(ax+b) , donde a y b son números reales.

– a) Calcule los valores de a y b para que la función tenga un extremo relativo en el punto (3,e^3)
– b) Para los valores de a y b obtenidos, diga qué tipo de extremo tiene la función en el punto citado.


  •  (1883) Ejercicios Resueltos
1º BACH. CIENCIAS 1º BACH. SOC. 1º ESO 2º BACH. CIENCIAS 2º BACH. SOC. 2º ESO 3º ESO 4º ESO