EJERCICIOS RESUELTOS - Geometría en el Espacio
Ejercicios de Geometría en el espacio. Bachillerato
Dados los puntos ![]() y
y ![]() , escriba las ecuaciones paramétricas, continua e implícitas de la recta que pasa por los puntos
, escriba las ecuaciones paramétricas, continua e implícitas de la recta que pasa por los puntos ![]() y
y ![]()
Dados los vectores ![]() ,
, ![]() y
y ![]() , se pide:
, se pide:
– a) ¿Son linealmente dependientes los 3 vectores?
– b) Calula ![]() (producto vectorial)
(producto vectorial)
– c) Encuentra dos vectores paralelos al vector ![]()
– d) Encuentra dos vectores perpendiculares al vector ![]()
– e) Halla el ángulo que forman los vectores ![]() y
y ![]()
Calcula las coordenadas de un vector ![]() de módulo 5 que sea perpendicular al mismo tiempo a los vectores
de módulo 5 que sea perpendicular al mismo tiempo a los vectores 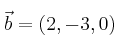 y
y ![]() , expresados respecto de la misma base ortonormal que el vector
, expresados respecto de la misma base ortonormal que el vector ![]()
Dados los vectores ![]() ,
, ![]() y
y ![]() , se pide:
, se pide:
– a) ¿Son linealmente dependientes los 3 vectores?
– b) Calula ![]() (producto vectorial)
(producto vectorial)
– c) Encuentra dos vectores paralelos al vector ![]()
– d) Encuentra dos vectores perpendiculares al vector ![]()
– e) Halla el ángulo que forman los vectores ![]() y
y ![]()
Consideramos los puntos ![]() ,
, ![]() y
y ![]() .
.
– a) Calcula ![]() (distancia entre los puntos A y B)
(distancia entre los puntos A y B)
– b) 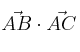 (producto escalar)
(producto escalar)
– c) Calcula el perímetro del triángulo de vértices A, B y C
– d) Halla el área del triángulo de vértices A, B y C
Halla dos puntos y dos vectores directores de la recta
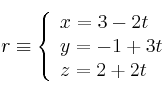
Halla dos puntos y dos vectores directores de la recta
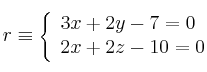
Halla la ecuación del plano que pasa por los puntos ![]() ,
, ![]() y
y ![]()
Dados los puntos ![]() ,
, ![]() y
y ![]() , se pide:
, se pide:
– a) Ecuación del plano ![]() que pasa por
que pasa por ![]() ,
, ![]() y
y ![]()
– b) Vector normal al plano ![]()
– c) Ecuación de una recta perpendicular al plano ![]() y que pase por el punto
y que pase por el punto ![]()
La Gran Pirámide de Guiza (también conocida como Pirámide de Keops o de Jufu) es la más antigua de las siete maravillas del mundo y la única que aún perdura, además de ser la mayor de las pirámides de Egipto. Ayúdanos a conocer un poco más de la Gran Pirámide, siguiendo los siguientes pasos:
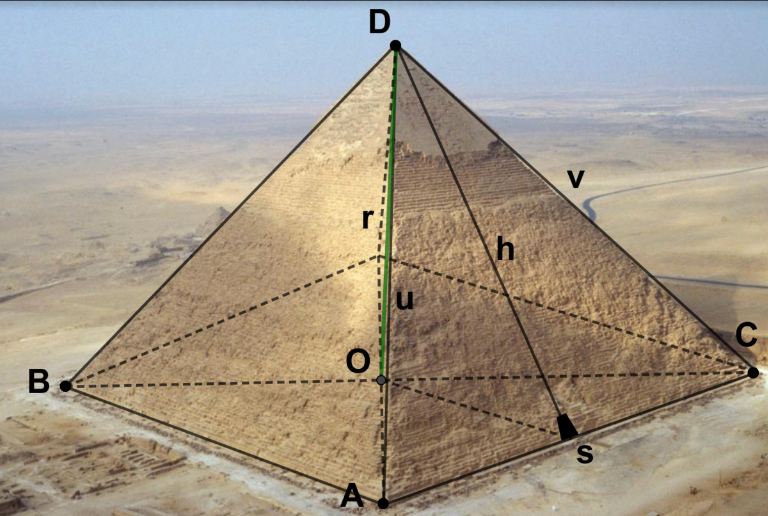
1) La base de la pirámide está formada por los cuatro puntos de los cuales tres puntos son ![]() ,
, ![]() y
y ![]() . Forma los vectores
. Forma los vectores ![]() y
y ![]() , comprueba que son linealmente independientes y calcula el área del paralelogramo que forman haciendo uso del producto vectorial. Sabiendo que la longitud es
, comprueba que son linealmente independientes y calcula el área del paralelogramo que forman haciendo uso del producto vectorial. Sabiendo que la longitud es ![]() y por tanto la superficie es
y por tanto la superficie es ![]() ¿Cuántos metros cuadrados de superficie tiene la Gran Pirámide?
¿Cuántos metros cuadrados de superficie tiene la Gran Pirámide?
2) Si la vertical del centro de la pirámide sigue esta ecuación:
![]()
Y el lado de la puerta (donde está el ![]() ) es la recta de ecuación:
) es la recta de ecuación:
![]()
¿Cuántos metros hay de la puerta al centro de la pirámide, O? Demuéstralo con la distancia entre dos rectas (1=23 m)
3) Sabiendo que la cúspide (D) está en el ![]() calcular las ecuaciones vectoriales y paramétricas de las dos rectas
calcular las ecuaciones vectoriales y paramétricas de las dos rectas ![]() y
y ![]() que forma los lados (
que forma los lados (![]() y
y ![]() )
)
4) Halla el plano que contiene a la puerta ![]() y es un lado de la pirámide. Halla el plano que es vertical y contiene a la puerta y al centro O. Interseca ambos planos obteniendo la ecuación de la recta
y es un lado de la pirámide. Halla el plano que es vertical y contiene a la puerta y al centro O. Interseca ambos planos obteniendo la ecuación de la recta ![]() . Comprueba que es la misma recta que pasa por la puerta y la cúspide D.
. Comprueba que es la misma recta que pasa por la puerta y la cúspide D.
 Matemáticas IES
Matemáticas IES